標準差的應用

17.6 理解涉及標準分和正態分佈的現實生活問題中 標準差的應用 (Understanding the Applications of Standard Deviation to Real-life Problems involving Standard Scores and the Normal Distribution)

標準差嘅值除咗可以用嚟量度數據離差嘅之外， 標準差的應用 喺統計上亦十分之更重要。

• 喺HKDSE課入面就要求我哋識標準差喺標準分同正態分佈上嘅應用。

17.6.1  標準分 (Standard Score)

標準分嘅槪念其實好簡單，就係將一個數據嘅值“標準化”。

我哋可以用以下嘅例子嚟理解標準分嘅用途：

• 小明上學期數學考試嘅分數喺80分。因為想考好D，所以小明請咗補習老師幫佢補數。結果下學期考試分數係75分。
• 咁到底補習對小明係唔係冇幫助呢？
  • 就咁睇就好似係冇幫助。
  • 但如果上學期班入面嘅平均分係85分、而下學期考試班嘅平均分係70分，咁又好似唔同講法（因為小明補習後嘅分數變得比平均分高）。
  • 當然，上面嘅例子好似極端咗少少。
    咁如果上學期考試班入面嘅平均分係70分、而下學期考試班嘅平均分係65分呢？小明兩次嘅分數都係高過平均分10分。咁又點呢？
    • 喺依個時候我哋就可以先將小明兩次嘅分數“標準化”，然後再作比較。

通常標準分會用 z 嚟代表，而標準分嘅計算方法係：
\(\quad z=\dfrac{x-\bar{x}}{\sigma}\)

• 當中 \(x\)係別個數據原來嘅值（原值）
  　     \(\bar{x}\) 係數據組嘅平均值
  　     \(\sigma\) 係數據組嘅標準差
  • 由以上嘅公式我哋可以見到標準分其實係講緊“某個數據嘅值同平均數嘅距離係幾多個標準差”，而標準分嘅正負就代表咗數據嘅原值喺高過定低過平均分。
  • 用返小明數學考試嘅例子。如果，第一次成班嘅平均分係70分，而標準差係5分。而第二次成班嘅平均分係65分，而標準差係3分。
    • • 咁小明第一次數學考試嘅標準分 = (80 – 70) / 5 = 2
      • 而小明第二次數學考試嘅標準分 = (75 – 65) / 3 = 5
      • 因為小明嘅標準分有所提升，所以補習對小明嚟講應該有用。

總結：透過以標準差作單位嚟量度數據與嘅平均數嘅距離，標準分往往能消除一D環境因素（例如考試卷嘅深淺）、從而更有意思地表達出該數據嘅喺數據組內嘅高低。

17.6.2 正態分佈 (Normal Distribution)

正態分佈簡單嚟講就係“正常”嘅分佈。

• 而所謂嘅正常亦可以話係“最常見”或者大家都“期望係咁”嘅分佈情況。

要理解咩係正態分佈，我哋先睇吓以下嘅假設例子。

• 假設香港成年人嘅平均身高係165cm。我哋隨機抽出5000成年人量度身高。
• 如果我哋將數據每10cm分一組。我諗你好自然都會認為：
  • 最多人嘅組別會係“160cm – 169cm”嗰組（因為平均數喺依組入面）。
  • “170 – 179cm”嗰組應該會比““180 – 189cm”嗰組多人。
    • 即距離平均數越遠，組別內嘅人數就會越少。
• 其實你有咁嘅認同係因為你一早就接受咗上嘅身高係“正常咁分佈”。

下面顯示咗幾個“同自然有關”嘅統計數據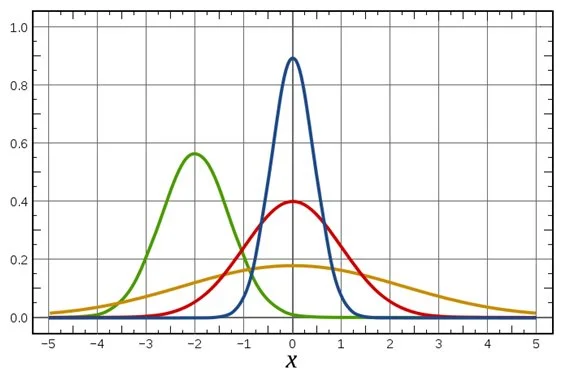

• x-軸可以睇成為數據嘅值、而y-軸係數據嘅頻數（至於D數據內容、單位喺咩大家唔駛理）
• 我哋發現幾個數據分佈圖形狀都差唔多，而且仲有以下嘅特點：
  • 分佈曲線圖為鐘形（bell-shaped）
  • 分佈曲線圖對稱於平均值
  • 平均值、中位數同眾數嘅值相等
    （即圖中各線曲線最高嗰點）

正態分佈可以話係一個喺各領域（包括數學、物理、生物、工程及統計等等）都非常重要、經常出現嘅數據分佈情況。

• 其實只要數據量大，好多嘢都係擁有一個正態分佈嘅。例如：
  • 人嘅身高、體重、壽命等等
  • 一般公開試嘅學生成績（要指明公開試係因為喺公開試先會有大量嘅考生）
  • 工廠生產嘅“5公斤米”嘅實際重量（5公斤只係一個期望值，但每包米都可以有少少偏差）。
• 不過喺中學文憑嘅必修部份，我認為大家唔需要詳細學咩係正態分佈。
  • 大家只要對正態分佈有個概念、知邊佢係鐘形就OK。（當然仲要學有關標準差喺正態分佈嘅應用。）

17.6.3 在正態分佈上 標準差的應用 (Applications of Standard Deviation in Normal Distibution)

對於一組正態分佈嘅數據，數學家發現當知道咗數據組嘅平均數（留意正態分佈數據嘅平均數、眾數同中位數係相等嘅）同標準差之後，可以得到如下圖所示的同一結果：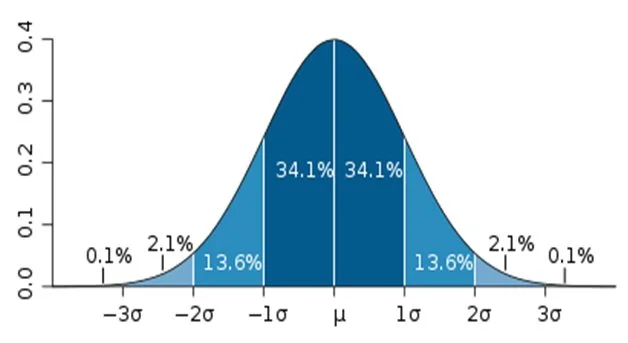

• 約2% 嘅數值分佈喺距離平均值有1個標準差之內嘅範圍
• 約4% 嘅數值分佈喺距離平均值有2個標準差之內嘅範圍
• 約7% 嘅數值分佈喺距離平均值有3個標準差之內嘅範圍

舉個例子：某次數學公開考試內，考生嘅平均分係70分、而標準差係8分。

• 平均分 + 3 x 標準差 = 70 + 3 x 8 = 94分
• 平均分 – 3 x 標準差 = 70 – 3 x 8 = 46分
• 因此我哋可以推論出有約7%的考生成績應在46分至94分內。

如果諗深一層，可能你會問：“既然D數據都知邊晒，咁如果想知有幾多個%嘅數據喺咩範圍內，其實數一數都得啦”。

• 冇錯。但其實以上只係解釋標準差嘅大細可以用嚟指出數據嘅分散嘅集中度。
• 標準差更加重要嘅應用係喺統計入面。

舉個例子嚟解釋標準差喺統計內嘅應用

• 某機構做咗個“香港成年人高身”嘅統計調查。
• 第一次調查時訪問咗100人。
  • 結果如下：數據嘅範圍係“165cm至 185cm”、平均數175cm、標準差係10cm。
  • 而機構就發表以下嘅結論：
    • 香港人平均身高係175cm，絕大部份人嘅高身係喺“165cm至 185cm”內。
  • 睇落好似冇咩問題。但其實“165cm至 185cm”只係“平均值+/- 1個標準差嘅範圍”，所以機構最多只可以講“約七成人嘅身高係喺165cm至185cm內”。
    • 但“七成”又好似唔夠準、冇咩特別意思。
• 機構結果做咗第二次調查。今次訪問咗10000人。
  • 結果如下：數據嘅範圍係“150cm至 189cm”、平均數174cm、標準差係5cm。
  • 雖然數據嘅範圍大咗，但標準差就細咗。而機構就可以發表以下嘅結論：
    • 香港人平均身高係174cm，約95%人嘅高身係喺“164cm至 185cm”內。
• 由此我哋可以見到“統計數據嘅標準差對一個統計嘅可信性有好大影響”。