從不同角度理解函數f(x)的變換
9.4 從表列、符號和圖像的角度理解 函數的變換 (Understand the Transformation of the Function f(x) from Tabular, Symbolic and Graphical Perspectives)
函數的變換 其實係對一個函數f(x)進行一D數學上嘅“改動”而得出一個新函數。
- 至於新函數同舊函數嘅關係,我哋通常會基於新、舊函數嘅圖像嚟作比較。
- 喺依課入面,我哋會用嘅函數f(x) 都會係“x2 – x – 6”。咁做係想大家可以由同一個函數出發而對函數作出變換。
9.4.1 函數的變換:上下移動 / 把圖像 y=f(x) 作上下移動(Translating the Graph Upwards/Downwards)
仲記唔記得我哋點用表列(即用下面個表)嚟幫我哋畫 y = x2 – x – 6 嘅圖像?
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 6 | 0 | -4 | -6 | -6 | -4 | 0 | 6 |
如果我哋要將個圖像向上移四格,好明顯我哋要睇將每一個y值都“加4”。
- 如果用表列嚟表示,我哋就會有下面嗰表:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| f(x) | 6 | 0 | -4 | -6 | -6 | -4 | 0 | 6 |
| f(x)+4 | 10 | 4 | 0 | -2 | -2 | 0 | 4 | 10 |
- 而新、舊嘅圖像就會好似下面幅圖咁:
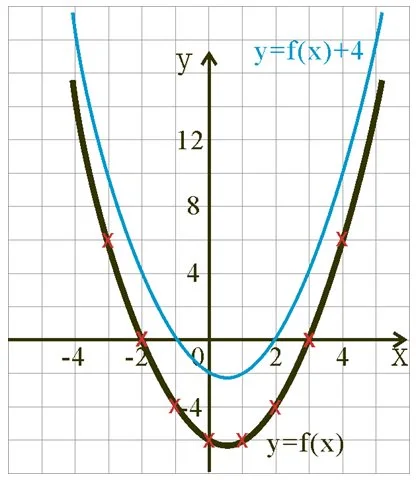
- 用符號嚟表達嘅話,個新函數就係 f(x) + 4。
§總結:
- 如果將圖像 y = f(x) 上移k格,咁新函數圖像嘅符號式係 y = f(x) + k。
- 如果將圖像 y = f(x) 下移k格,咁新函數圖像嘅符號式係 y = f(x) – k。
9.4.2 把圖像 y=f(x) 作左右移動(Translating the Graph to the Left/Right)
如果我哋要將個圖像向左移兩格,好明顯新、舊嘅函數圖像如好似下面幅圖咁:
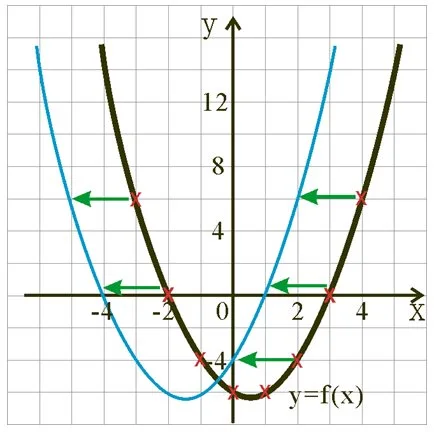
睇返舊函數嘅表列:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 6 | 0 | -4 | -6 | -6 | -4 | 0 | 6 |
而根據個新函數嘅圖像,我哋可以見到新函數嘅表列係(我哋暫叫個新函數做 g(x)):
| x | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 |
| y | 6 | 0 | -4 | -6 | -6 | -4 | 0 | 6 |
假如我哋將新、舊函數嘅y值一欄一欄咁對齊(留意上面嘅表列嘅紅色的欄位),我哋會發現相應嘅x-值都係相差2。即:
g(0) = f(2);
g(1) = f(3);
g(2) = f(4);
由此我哋可以推論出: g(x) = f(x + 2)
§ 總結:
- 如果將圖像 y = f(x) 左移k格,咁新函數圖像嘅符號式係 y = f(x + k)。
- 如果將圖像 y = f(x) 右移k格,咁新函數圖像嘅符號式係 y = f(x – k)。
§ 唔似得將圖像作上下移動,好多同學都會將f(x + k)同f(x – k)撈亂。我建議大家要練習吓用以下嘅想法去作出判斷:
- 想像舊嘅圖像經過一點(5, 8)。咁即係當x=5時,y = f(5) = 8。
- 如果新函數g(x)嘅圖像要向左移2格,咁即係話當x = 3時,y = g(3) = f(5) = 8。
- 咁即係話 g(3) = f(3 + 2),所以 g(x) = f(x + 2)
- 如果新函數h(x)嘅圖像要向右移3格,咁即係話當x = 8時,y = h(8) = f(5) = 8。
- 咁即係話 h(8) = f(8 – 3),所以 h(x) = f(x – 3)
- 當然,如果你話“我唔會記錯嘅!”,咁你的確只要記住上面個總結就冇問題。
9.4.3 把圖像 y=f(x) 沿y-軸作伸展或縮少 (Stretching/Compressing the Graph across y-axis)
沿y-軸作縮少(例如縮少一半)其實就好似我哋用哈哈鏡將幅圖上下壓扁。
- 如果用表列嚟表示,我哋就會有下面嗰表:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| f(x) | 6 | 0 | -4 | -6 | -6 | -4 | 0 | 6 |
| f(x)/2 | 3 | 0 | -2 | -3 | -3 | -2 | 0 | 3 |
- 而新、舊嘅圖像就會好似下面幅圖咁:
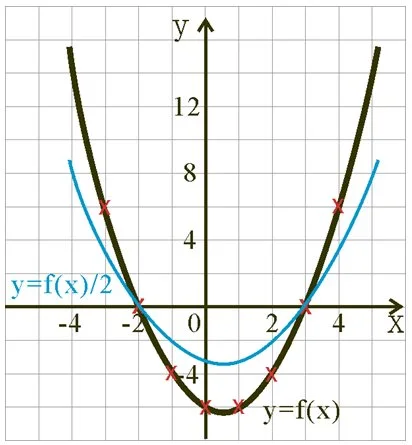
- 用符號嚟表達嘅話,個新函數就係 f(x)/2 (亦可以話係 (1/2)f(x))。
唔難想像如果我哋將幅圖“沿y-軸作伸展一倍”,個新函數會係 2f(x)。
§ 總結:
- 如果將圖像 y = f(x) 沿y-軸作伸展或縮少,咁新函數圖像嘅符號式係 y = kf(x)。
- 當 0 < k < 1時,圖像就會作縮少。
- 當 k > 1時,圖像就會作伸展。
9.4.4 把圖像 y=f(x) 沿x-軸作伸展或縮少 (Stretching/Compressing the Graph across x-axis)
同“沿y-軸作伸展”相似,“沿x-軸作伸展”(例如伸展一半)就係將幅圖左右咁壓扁。
- 首先我哋睇吓下面嗰表(記住f(x) = x2 – x – 6):
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| f(x) | 14 | 6 | 0 | -4 | -6 | -6 | -4 | 0 | 6 |
| f(x/2) | 0 | -4 | -6 | -6 | -4 |
- 而新、舊嘅圖像就會好似下面幅圖咁:
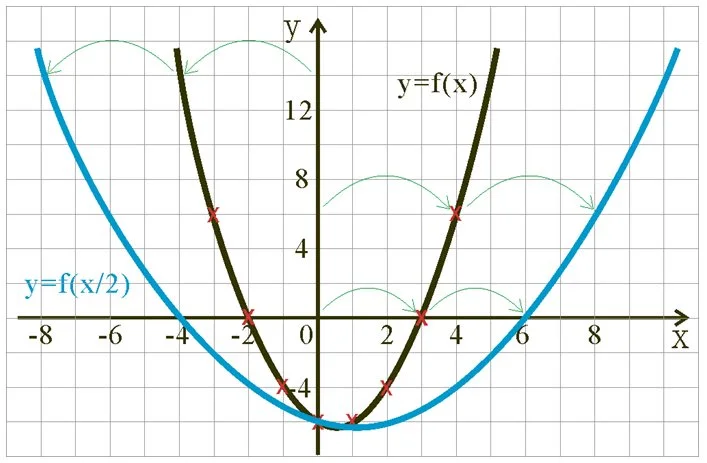
留意舊圖嘅每一點同x-軸嘅距離就好似放大咗一倍咁(如圖中綠色箭咀所示)。
- 用符號嚟表達嘅話,個新函數就係 f(x/2)。
唔難想像如果我哋將幅圖“沿x軸作縮少一倍”,個新函數會係 f(2x)。
§ 總結:
- 如果將圖像 y = f(x) 沿x-軸作伸展或縮少,咁新函數圖像嘅符號式係 y = f(kx)。
- 當 0 < k < 1時,圖像就會於水平方向作放大。
- 當 k > 1時,圖像就會於水平方向作縮少。
9.4.5 把圖像 y=f(x) 沿x-軸或y-軸作反射 (Reflecting the Graph in x-axis/y-axis)
“反射”亦可以被形容為“沿住x-軸上下倒轉”或“沿住y-軸左右反轉”。
- 我哋先考慮以下嘅表:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| f(x) | 6 | 0 | -4 | -6 | -6 | -4 | 0 | 6 |
| -f(x) | -6 | 0 | 4 | 6 | 6 | 4 | 0 | -6 |
- 新、舊嘅圖像就會好似下面幅圖咁:
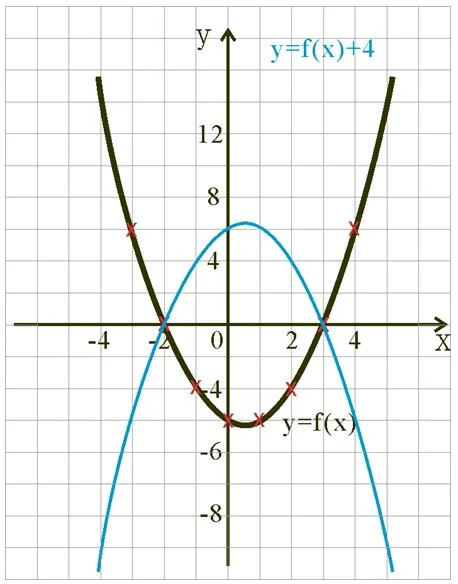
- 由此可見“沿x-軸作反射”後嘅新函數圖像係 y = – f(x)。
唔難想像如果我哋將幅圖“沿y-軸作反射”,個新函數會係 f(– x)。
§ 總結:
- 如果將圖像 y = f(x) 沿x-軸作反射,咁新函數圖像嘅符號式係 y = – f(x)。
- 如果將圖像 y = f(x) 沿y-軸作反射,咁新函數圖像嘅符號式係 y = f(– x)。
其實反射可以話係以前學過咗“把圖像 y=f(x) 沿x-軸或y-軸作伸展或縮少”嘅一個特別情形。
- 當中y = k f(x)及y = f(kx) 嘅k 值係 “–1”。
- 再推論落去,我哋會發現如果k值係“–2”, 咁y = -2 f(x) 其實係會有一個“沿x-軸作反射後再沿y-軸伸展一倍”嘅效果。
- 這亦可以睇成係因為“–2 = (-1) x 2”。
