指數函數與對數函數圖像 » 指數及對數 » DSE Maths筆記

3.4 理解指數函數與對數函數的性質及認識其圖像的特徵 (Understand the Properties of Exponential Functions and Logarithmic Functions and Recognise the Features of their Graph)

提到指數函數與對數函數圖像，同學多數都係唔明，或只係記得佢地有鏡射嘅關係。咁係因為好多補習天王都會教大家依個”秘技”。但同學往往只係睇show咁睇，根本唔明。其實更重要嘅係理解個別圖像嘅特徵，然後再睇兩者嘅關係，咁你就會好自然咁睇到個鏡射。

指數函數係\(a^{x}\)

指數函數嘅圖像係 \(y=a^{x}\) 嘅圖像

下面圖中就有三個例子：
- \(y=(0.5)^{x}\) (綠色線)
- \(y=(1.5)^{x}\) (紅色線)
- \(y=(2)^{x}\) (藍色線)

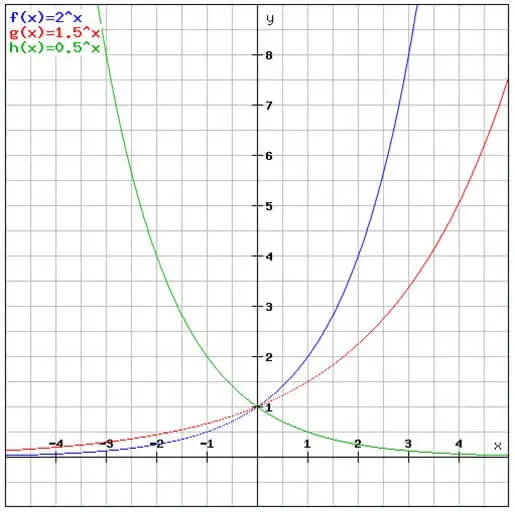
要明白同理解“指數函數嘅圖像”個樣其實唔太難，只要明白幾點就ok：

無論a等於咩都好，a⁰ 永遠等於 1（即a⁰=1）。
- 所以當x=0時，y = a⁰ = 1。即所有指數函數嘅圖像都會通過 (0, 1)依點。
先假設x係正整數(即考慮y-軸右邊圖像嘅樣)，咁a^x 就等於“a自己乘自己幾多次”
- 例如\(a^{x} = x \times x \times x\)。
- 當 a > 1 嘅時候，a自己乘自己次數越多，個數就會越大。
  - 所以對 \(y=(1.5)^{x}\) 同 \(y=(2)^{x}\) 兩個圖像嚟講，當x增加時，y亦會增加。
- 當0 < a < 1嘅時候，a自乘次數越多，個數就會越細。
  - 所以對\(y=(0.5)^{x}\) 圖像嚟講，當x增加時，y會減少。
    - 所以當x好大嘅時候，y會好接近0。
- a < 0 依種情況係唔會考嘅！
當x係負數嘅時候(即考慮y-軸左邊圖像嘅樣)，\(y=a^{負數值} = \dfrac{1}{a^{正數值}}\)。根據上面嗰點：
- 當a > 1嘅時候，負數值越負， \(a^{正數值}\)會越大，
  即\(\dfrac{1}{a^{正數值}}\)會越接近0。
- 當0 < a < 1嘅時候，負數值越負， \(a^{正數值}\)會越接近0，
  即\(\dfrac{1}{a^{正數值}}\)會好大。
另外比較圖像\(y=(1.5)^{x}\)同 \(y=(2)^{x}\)，大家會發覺\(y=(2)^{x}\)嘅圖像係升得快過\(y=(1.5)^{x}\)嘅圖像。
- 依個其實好易理解。\(a^{x} = a自己乘自己x咁多次\)，
  所以每當x增加1嘅時候：
  - 對\(y=(1.5)^{x}\)嚟講只係“乘多一個5”
  - 但對\(y=(2)^{x}\)嚟講就“乘多一個2”。更係大得快d啦！

對數函數係\(log_{a}x\)

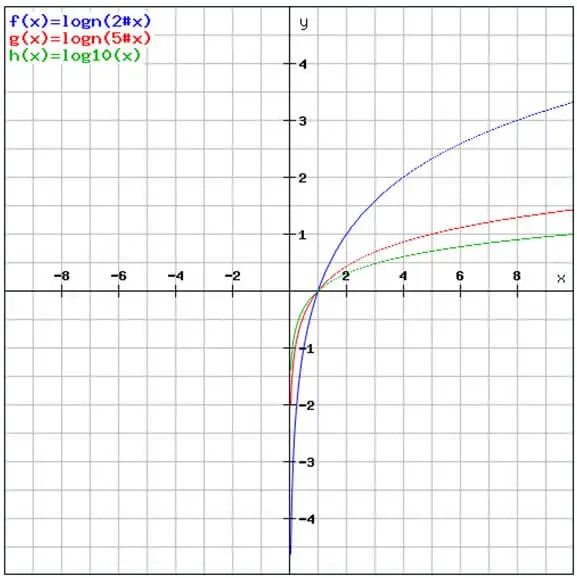
要明白同理解“對數函數嘅圖像”個樣其實唔太難，只要明白幾點就ok：

無論a等於咩都好，a⁰ 永遠等於 1（即a⁰=1）。
- 所以當x=1時，y = log_a 1 = 0。即所有對數函數嘅圖像都會通過 (1, 0)依點。
因為 log_a a = 1，而log_a aⁿ = n (log_a a) = n。所以例如對y = log₂ x嚟講：
- 當x=2時，y = log₂ 2 = 1；　當x=4時，y = log₂ 4 =log₂ 2² = 2
  當x=8時，y = log₂ 8 = log₂ 2³ = 3。
  所以y = log₂ x嘅圖像會經過 (2, 1)、(4, 2)、(8,3)、(16,4)等點。
而對y = log₁₀ x嚟講：
- y = log₁₀ x嘅圖像會經過 (10, 1)、(100, 2)、(1000,3)、(10000,4)等點
- 大家可以見到y = log₂ x嘅圖像係升得快過y = log₁₀ x嘅
用計數機計“一個負數嘅log”係會“maths error”嘅！
- 咁係因為log _a x嘅定義域係　0
- 所以對數函數嘅圖像係唔會喺y-軸左邊嘅

喺下邊圖中有三個圖像：

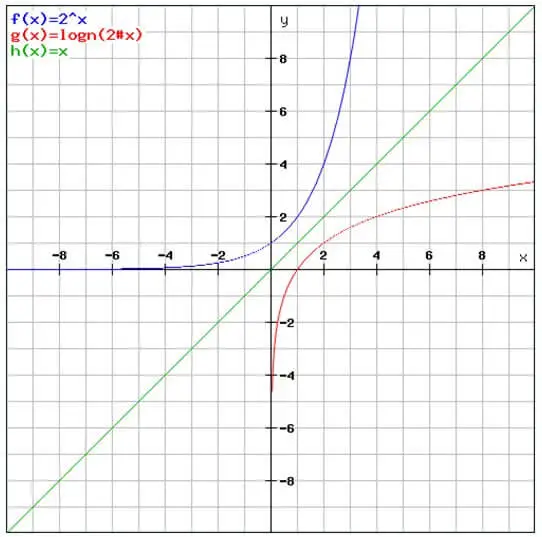
依個就係喺“課程指引”入面所講嘅“y=a^x 與 y = log_ax 對稱於 y = x”

§大家如果唔明就無謂強求去背。因為當中嘅解釋係比較深，而且我覺得依點喺長題目度出嘅機會唔大。