理解直線方程
10.1 理解直線方程 (Understand the Equation of a Straight Line)
可能你會話: 「一條直線無論你點畫佢都係一條直線,都唔知有咩要去理解??」
其實要你 理解直線方程 即係要你睇得計條直線嘅方程出嚟。
10.1.1 求直線方程的方法 (Methods of Finding the Equation of a Straight Line)
根據中學文憑數學嘅課程,大家要識得喺知道以下嘅條件嘅情況下求直線嘅方程:
- 直線上任意兩點的坐標
- 直線的斜率及該直線上一點的坐標
- 直線的斜率及其y截距
但無論係詳情況都好,只要題目要我地去求一條直線嘅方程,我哋都要先搵到以下兩樣嘢:
- 條直線嘅斜率 (當計到等於m)
- 直線上其中一點嘅坐標 (當嗰點係 (x1 , y1))
搵到“直線嘅斜率”同“直線上其中一點嘅坐標”之後,條直線嘅方程就會係:
\(\dfrac{y-y_1}{x-x_1} = m\)
- 當然,考試嘅時候多數m同(x1 , y1)會係實數,所以我哋可以將條方程化簡。
\(\begin{align}
\dfrac{y-3}{x-1} &= -1 \\
y-3 &=-x+1\\
x+y-2 &=0
\end{align}\)
答: 該直線的方程為 x + y – 2 = 0
10.1.2 求直線斜率的方法
做“求直線方程嘅題目”時最重要嘅一步可以話係“計直線嘅斜率”。
求直線斜率嘅方法基本上有五個:
- 利用兩點已知點嘅坐標,代入公式 斜率 \(m = \tfrac{y_2-y_1}{x_2-x_1}\)
- 利用“如兩條線平行,則它們的斜率相等”,即 m1 = m2
- 利用“如兩條線互相垂直,則 \(m_1 \times m_2=-1\)”
- 利用斜率 \(m=tan\theta\)
(其中θ為“由x-軸開始以逆時鐘方向度起至直線的夾角”)- 例子:下圖中直線的斜率 = tan135o = -1
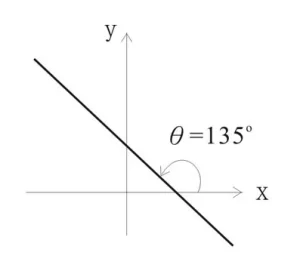
- 例子:下圖中直線的斜率 = tan135o = -1
- 把直線已知的方程改寫成 y = mx + c 的形式 (即做一次主項變換)。
- 直線的斜率 = m (即右邊x項的系數)
10.1.3 由直線方程描述直線的特徵 (Describing the Features of a Straight Line from its Equation)
希望嚟到依度,大家已經接受到以下幾點:
- 直線方程嘅形式係 ax + by + c = 0 (當中a,b及c為數字)。
- 要定出一條直線,我哋要定出直線嘅斜率同直線通過嘅其中一點。
- 一條直線比較特別嘅點係x-軸同y-軸上嗰兩點(即x-軸截點同y-軸截點)。
當我哋要由一條直線方程嚟描述一條直線嘅特徵嘅時候,我哋就一定先要做以下嘅嘢:
- 將直線嘅方程由ax + by + c = 0變成 y = mx + c。
- 留意兩條式入面嘅c只係符號相同,佢哋嘅值並唔相等!
有咗y = mx + c條式,我哋要知道條直線嘅“斜率”、“x-軸截距“同“y-軸截距”可以話係易如反掌。
- m其實係我哋通常用嚟代表斜率嘅符號,既然條式都叫“y = mx + c”,所以好易記:
- 直線斜率 = m。
- y-軸截點嘅特點係“x-坐標 = 0”。代x=0入條式度我哋會計到 “y = c”。所以:
- y-軸截距 = c (即y-軸截點 = (0, c))
- x-軸截點嘅特點係“y-坐標 = 0”。代y=0入條式度我哋會計到 “x = -c/m”。所以:
- x-軸截距 = -c/m (即x-軸截點 = (-c/m, 0))
另外一樣要識嘅就係要知道點測試一點係唔係喺條直線上面。
- 其實方法冇咩特別。當我哋要試吓點 (3, 5) 係唔係喺條直線上面。
- 我哋只要代x=3入條直線嘅方程度,睇吓計到嘅y-值係唔係5就可以。
- 當然,如果計到嘅y-值係等於5,咁(3, 5)就係喺條直線上面。
- 以上嘅方法根本就係用嚟測試“一點係唔係喺一個圖像y=f(x)上”嘅方法。
- 我哋只要代x=3入條直線嘅方程度,睇吓計到嘅y-值係唔係5就可以。
- 另一個方法就係把要測試嘅點嘅 x、 y坐標代入方程, 睇吓左邊 LHS (left hand side) 是否與等同於RHS。如等同,即點在直線上
| x | 0 | 3 | 6 |
| y | 2 | 4 | 6 |
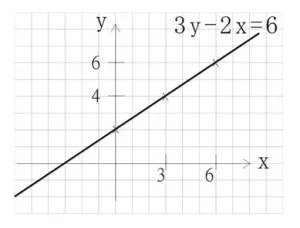 將“3y – 2x = 6”改寫成 y = mx + c 的格式:
\(y = \tfrac{2}{3}x + 2\)
將“3y – 2x = 6”改寫成 y = mx + c 的格式:
\(y = \tfrac{2}{3}x + 2\)
- 直線斜率 = m = 2/3 從右圖中,大家要留意正嘅斜率係“斜向邊一面”(由左下角向右上角走);負嘅斜率就會“斜向另一面” (由左上角向右下角走)。
- y-軸截距 = c = 2
- x-軸截距 = -c/m = -2/(2/3) = -3 (這與從圖中所睇到嘅係一樣)
- 先代x=3入條式同,我哋會計到 y = 4。
- 所以點(3,6)唔係喺條線上面。 (這與從圖中所睇到嘅係一樣)
- 當然另一方法是把 x=3, y=6代入原方程 3卜- 2= 6,
- LHS = 3(3) – 2(6) = 9 – 12 = -3 ≠ RHS 所以(3, 6)不在直線上。
